As mentioned in previous phase the ray-sphere intersection function (calculateSphereIntersections) returned a list of intersection points even though it is enough to be aware of the closest intersection point only. Also, as pointed out by Boojum in the related reddit thread dynamic memory allocation in ray tracer inner loop hinders performance unnecessarily.

In order to tackle this and more the ray-sphere intersection function was revisited:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
std::pair<bool, Vector> calculateSphereIntersection(Vector rayOrigin, Vector rayDirection) {
  float sphereRadius = 0.5f;
  Vector l = sphereCenter - rayOrigin;
  float s = l.dot(rayDirection);
  float lSquared = l.dot(l);
  float sphereRadiusSquared = sphereRadius * sphereRadius;
  if (s < 0 && lSquared > sphereRadiusSquared) return std::make_pair(false, Vector());
  float mSquared = lSquared - (s * s);
  if (mSquared > sphereRadiusSquared) return std::make_pair(false, Vector());
  float q = sqrt(sphereRadiusSquared - mSquared);
  float t = 0.0;
  if (lSquared > sphereRadiusSquared) t = s - q;
  else t = s + q;
  return std::make_pair(true, spherePoint(rayOrigin, rayDirection, t));
}

The new version requires some explanation: Firstly the dynamic memory allocation is gone due to usage of std::pair which is allocated in stack. Otherwise the ray-sphere intersection algorithm is improved by following the optimized ray-sphere intersection solution explained in the book Real-Time Rendering by Tomas Möller and Eric Haines.

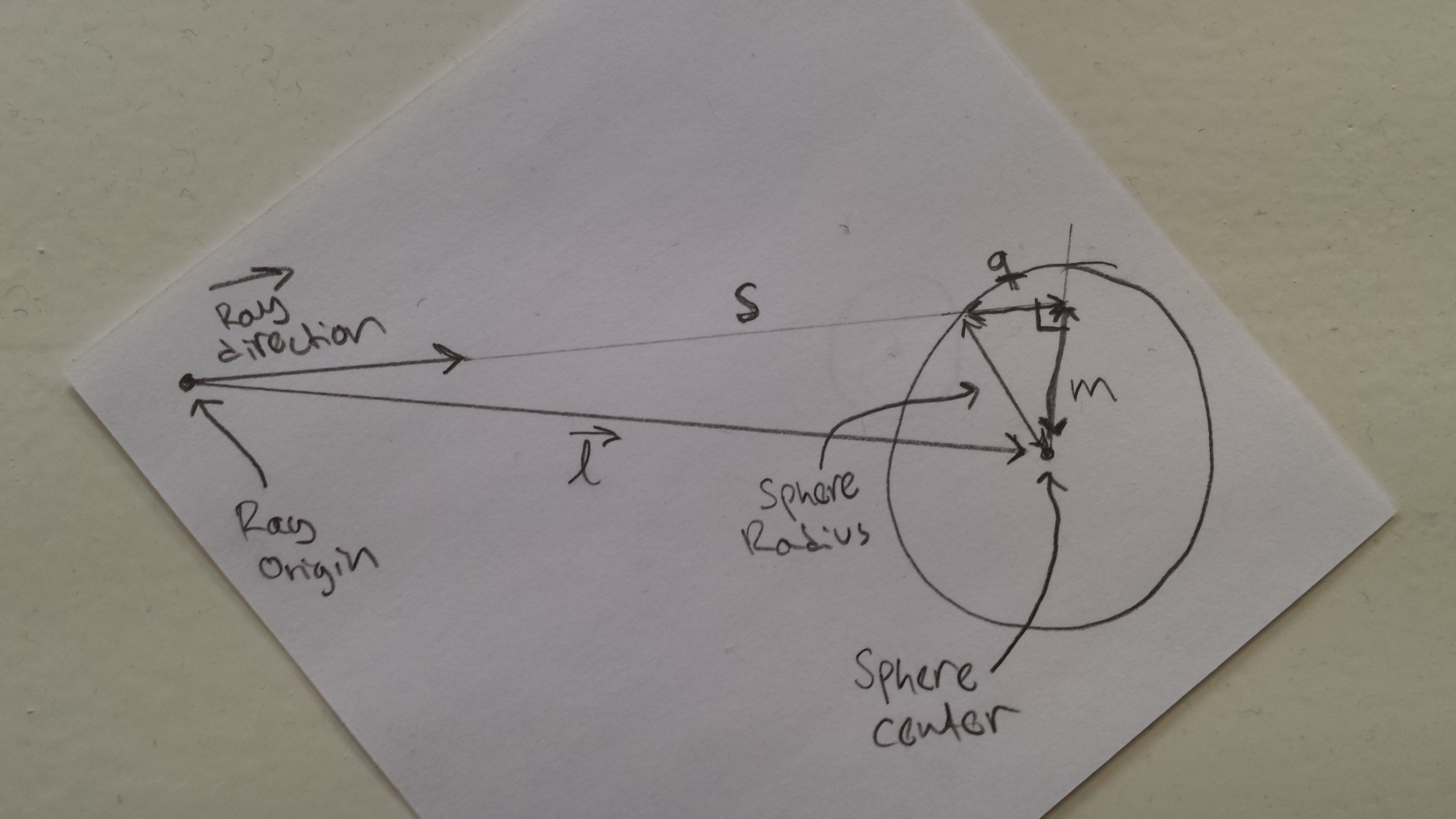
As shown in the image, l is the vector from ray origin to sphere center. s is projection of l on to ray direction vector. If s < 0 && lSquared > sphereRadiusSquared then sphere lies behind the ray origin and ray origin is not inside the sphere, thus there cannot be intersection and we can return. m is the distance between sphere center and the projection s and can be calculated using pythagorean theorem. If mSquared > sphereRadiusSquared then the distance between s and sphere center is more than sphere radius and the ray does not intersect with the sphere. Finally, q is the length of s that lies within sphere and can be calculated using pythagorean from sphere radius and m. If lSquared > sphereRadiusSquared then ray origin is outside sphere and t is s - q. Otherwise ray origin is within sphere and t is s + q.

See the phase 4 source code in github